The skyline of Singapore as viewed from the Marina Promenade (shown on the left) is one of the iconic scenes of Singapore. Country X would also like to create an iconic skyline, and it has put up a call for proposals. Each submitted proposal is a description of a proposed skyline and one of the metrics that country X will use to evaluate a proposed skyline is the amount of overlap in the proposed sky-line.

As the assistant to the chair of the skyline evaluation committee, you have been tasked with determining the amount of overlap in each proposal. Each proposal is a sequence of buildings, 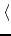b₁, b₂,..., b_n 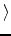, where a building is specified by its left and right endpoint and its height. The buildings are specified in back to front order, in other words a building which appears later in the sequence appears in front of a building which appears earlier in the sequence.

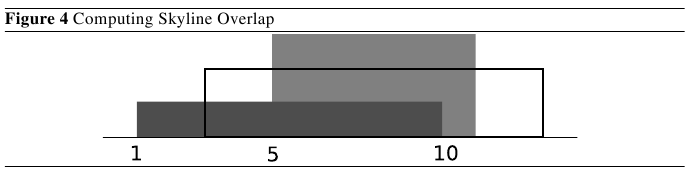
The skyline formed by the first k buildings is the union of the rectangles of the first k buildings (see Figure 4). The overlap of a building, b_i , is defined as the total horizontal length of the parts of b_i , whose height is greater than or equal to the skyline behind it. This is equivalent to the total horizontal length of parts of the skyline behind b_i which has a height that is less than or equal to h_i , where h_i is the height of building b_i . You may assume that initially the skyline has height zero everywhere.

Input 

The input consists of a line containing the number c of datasets, followed by c datasets, followed by a line containing the number `0'.

The first line of each dataset consists of a single positive integer, n (0 < n < 100000) , which is the number of buildings in the proposal. The following n lines of each dataset each contains a description of a single building. The i -th line is a description of building b_i . Each building b_i is described by three positive integers, separated by spaces, namely, l_i , r_i and h_i , where l_i and r_j (0 < l_i < r_i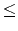100000) represents the left and right end point of the building and h_i (0 < h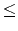109) represents the height of the building.

Output 

The output consists of one line for each dataset. The c -th line contains one single integer, representing the amount of overlap in the proposal for dataset c . You may assume that the amount of overlap for each dataset is at most 2000000.

Note: In this test case, the overlap of building b₁ , b₂ and b₃ are 6, 4 and 4 respectively. Figure 4 shows how to compute the overlap of building b₃ . The grey area represents the skyline formed by b₁ and b₂ and the black rectangle represents b₃ . As shown in the figure, the length of the skyline covered by b₃ is from position 3 to position 5 and from position 11 to position 13, therefore the overlap of b₃ is 4.

Sample Input 

1 
3 
5 11 3 
1 10 1 
3 13 2 
0

Sample Output 

14