
A spray graph of size 1
| F - Spray Graphs |
The
one who reads a lot and walks a lot,
sees a lot and knows a lot.
Miguel de Cervantes Saavedra
As you should know, a directed acyclic graph is a directed graph with no directed cycles. We define a spray graph as a directed acyclic graph with the following form:

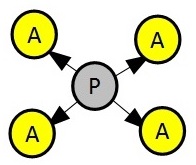
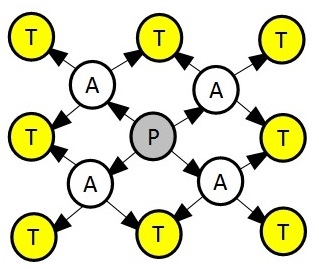
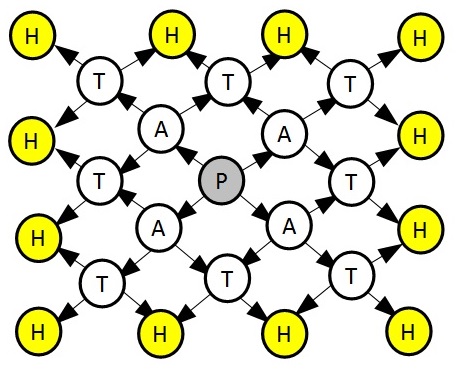
and so on.
You have to compute the number of different paths from the central node (the gray node, P) to any leaf node (yellow ones) in a spray graph of size n.
The first line of the input contains an integer, t, indicating the number of test cases. For each test case, one line appears containing an integer n, 1 ≤ n ≤ 30, representing the size of the spray graph.
For each test case the output should contain a single line, indicating the number of different paths from the central node to any leaf node in the corresponding graph.
4
1
2
3
4
1
4
12
28