|
I I U P C 2 0 1 4 |
|
|
Problem F: Light Combat Aircraft |
|
|
|
|
|
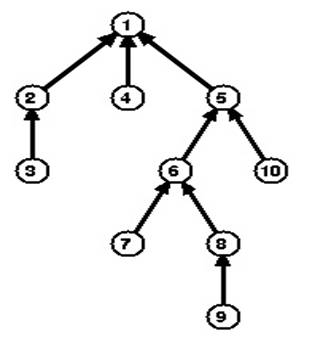
In graph theory. the lowest common ancestor (LCA) of two distinct nodes v and w in a rooted tree is the lowest (i.e. deepest) node that has both v and w as descendants, where we define each node to be a descendant of itself (so if v has a direct connection from w, w is the lowest common ancestor). For example, on the above tree (depicted from case 1) LCA( 3,5) = 1, LCA( 7,10 ) = 5, LCA( 6,5 ) = 5 etc. In this problem, given a Forest, i.e. a disjoint union of rooted trees, you have to find out for each node u how many distinct pair of nodes (v,w) exist such that LCA(v,w) would be u. You should assume that both (v,w) and (w,v) are same pair.
|
|
|
Input |
|
|
First line of input file contains number of test cases, T ≤ 100 and T cases follow. Each case starts with an integer N (1≤ N≤ 10000), number of nodes in the forest. Next line contains N integers, p1, p2, … pN ( 0≤ pi≤ N ), where pi is the parent of ith ( 1≤ i≤ N ) node in a rooted tree of the forest , If pi = 0 then node i is a root in rooted tree.
|
|
|
Output |
|
|
For each case, print the forest number starting from 1 and number of LCA pair for each node (ordered by node number) separated by space. See the sample output for exact formatting.
|
|
|
Sample Input |
Output for Sample Input |
|
4 10 0 1 2 1 1 5 6 6 8 5 3 2 0 0 4 0 1 2 1 4 0 1 0 3 |
Forest#1: 29 1 0 0 9 5 0 1 0 0 Forest#2: 0 1 0 Forest#3: 5 1 0 0 Forest#4: 1 0 1 0 |
|
|
|
|
Problem Setter: Prasanjit Barua Alternate Solution: Kayser Abdullah |
|
|
Output Explanation In case 2, in the given forest among the two trees rooted at 2 and 3, there is no pair for which LCA is 1 or 3. For pair (1, 2) LCA is 2. So, total pair for 2 is 1. In case 3, for pair (1,2), (1,3), (1,4), (2,4), (3,4) LCA is 1. For only pair (2,3) LCA is 2. There is no pair for which LCA is 3 or 4.
|
|
Note: Dataset is huge, so use faster I/O methods.