To Infinity and Beyond 

You probably don't know toys walk, play and talk when we are not around. And there are toys who can perform intergalactic missions! But lets forget about alien planets now, the toyland on earth is in danger, `Zurg' the evil emperor from outer world is planning to capture it. But as always when toyland is in trouble the great space ranger `Buzz Lightyear' of star command comes for the rescue!

Toyland consists of several cities and bidirectional roads. The Toyland chief wants to take following steps to save Toyland:

1. First divide the cities of Toyland into multiple regions. Two cities MUST be included in same region if there is at least one simple cyclic route connecting both cities. One city can be included in multiple regions. Size of each region should be maximal; that means extra city can't be added in a region. Here simple cyclic route means no vertex should appear more than one time in the route.
2. There are limited numbers of `Buzz' toys available. After creating the regions, one `Buzz' toy will be sent to each of them to save that region from Zurg!

Toys need energy to work. Each city can supply energy to infinite number of toys but the amount of energy a city provides daily to a single toy is limited otherwise toys may waste energy. A toy is assigned to a single region but it can get energy from any city within its region.

For a single toy, the total daily energy supply is the sum of the energy supply of all the cities within its region.

Each `Buzz' may need different amount of energy to work. If a region provides too less energy than additional energy need to be provided anyhow and it is considered as a loss. But if the region provides more energy than required, `Buzz' wastes it by playing with laser and flying all around. So:

Daily Loss in region X = | Daily Energy required by `Buzz' assigned in that region

- Daily Energy supplied by region X|

Exactly one `Buzz' must be assigned in each region, if there are more toy than needed, they'll keep them for emergency. The chief wants to minimize the maximum wastage among all the regions and he needs your help desperately.

Help the toyland to survive, expand your mind To Infinity and Beyond and find the answer.

Input 

First line of input will contain the number of test cases T$\le$600. For each case, first line will consist of number of cities N ( 1$\le$N$\le$100), roads E and number of Buzz toys available B ( 1$\le$B$\le$50). In next line there are N integers less than 1000, i-th integer denotes energy supply in city i. In next line there are B integers less than 1000, j-th integer denotes energy required by Buzz j. Next there are E lines each consisting two integer u and v denoting there is a bidirectional road between u and v (u$\ne$v). There is at most one road between two cities. All inputs are non-negative.

Output 

For each test case first print number of regions. Then, if number of regions is more than number of buzz available, output `No'; otherwise print the maximum wastage amount among all the regions. Print case number for every case, see sample output for details.

Output Explanation

Regions and optimal assignment in 1st case:

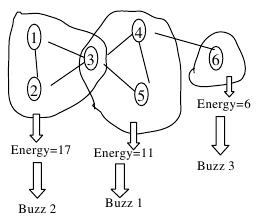
Note: Large input File, use faster I/O.

Sample Input 

2
6 7 3
5 4 8 1 2 6
10 14 9
1 2
2 3
3 1
3 4
4 5
3 5
5 6
4 3 1
5 4 8 1
10
1 2
2 3
3 1

Sample Output 

Buzz Mission 1: 3 3
Buzz Mission 2: 2 No

Problem Setter: Shafaet Ashraf
Alternate Solution: Shiplu Hawladar