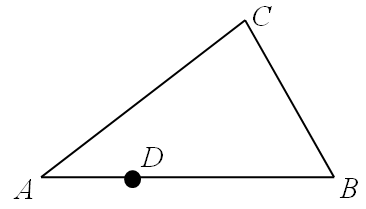
When I was a high school student, I learned that given a triangle ABC, denote D, E, F as the midpoints of AB, BC and CA, then three segments CD, AE, BF intersects at one point: the centroid.
Then I thought about the following question: if we change "midpoint" by "perimeter midpoint", can CD, AE, BF still intersect at one point?
To be precise, if CA+AD = DB+BC, we say D is the "perimeter midpoint" on AB.

It's not difficult to see that there is exactly one such point lying strictly inside the segment AB. Point E and F are defined similarly and also have unique positions.
Help (the younger) me to find out the answer!
The first line contains the number of test cases T(T<=100). Each test case contains 6 integers x1, y1, x2, y2, x3, y3, whose absolute values do not exceed 100. These integers represent three non-collinear points A(x1, y1), B(x2, y2), C(x3, y3).
For each test case, if CD, AE, BF intersect at one point, print the position of the intersection to 6 decimal places. Otherwise print "ERROR" (without quotes).
2 -1 0 1 0 0 1 0 0 5 0 3 3
Case 1: 0.000000 0.171573 Case 2: 2.362911 0.665041