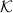 , inclusive, and satisfy the property that within each subset
no node is an ancestor1
of another. We will call these subsets the
, inclusive, and satisfy the property that within each subset
no node is an ancestor1
of another. We will call these subsets the 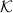 -anti-ancestral subsets of the tree.
-anti-ancestral subsets of the tree.
You will be given a connected undirected tree. Each node will have an associated integer that we will call its value. We also define the value of a subset of nodes as the sum of values of the nodes in the subset.
Consider the subsets of nodes of this tree whose size is between 1 and 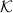 , inclusive, and satisfy the property that within each subset
no node is an ancestor1
of another. We will call these subsets the
, inclusive, and satisfy the property that within each subset
no node is an ancestor1
of another. We will call these subsets the 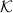 -anti-ancestral subsets of the tree.
-anti-ancestral subsets of the tree.
Your task is, given the tree, to find the 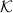 -anti-ancestral subset of maximum value.
-anti-ancestral subset of maximum value.
As an example, consider the tree below. Each node is named with a capital letter and the value of each node is the integer below the letter:
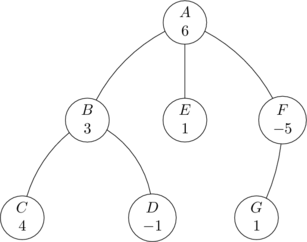
Suppose 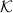 = 3. Then the subset of nodes {A}, {B, E}, {C, E}, {D, G} and {B, E, F} are some of the
= 3. Then the subset of nodes {A}, {B, E}, {C, E}, {D, G} and {B, E, F} are some of the
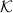 -anti-ancestral subsets of the tree, because they all have between 1 and
-anti-ancestral subsets of the tree, because they all have between 1 and 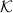 = 3 nodes and within each subset
there doesn’t exist a pair of nodes such that one is an ancestor of the other.
= 3 nodes and within each subset
there doesn’t exist a pair of nodes such that one is an ancestor of the other.
On the other hand, {A, B} is not a 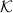 -anti-ancestral subset because A is an ancestor of B, {A, G} isn’t one
because A is an ancestor of G and {C, B, D} isn’t one either because B is an ancestor of both C and D. The
subset {C, D, E, F}, even though it doesn’t contain a node that is an ancestor of another one, is not a
-anti-ancestral subset because A is an ancestor of B, {A, G} isn’t one
because A is an ancestor of G and {C, B, D} isn’t one either because B is an ancestor of both C and D. The
subset {C, D, E, F}, even though it doesn’t contain a node that is an ancestor of another one, is not a
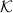 -anti-ancestral subset because it has 4 >
-anti-ancestral subset because it has 4 > 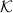 = 3 nodes. Similarly, the empty set ∅ is not one either because it
contains 0 elements.
= 3 nodes. Similarly, the empty set ∅ is not one either because it
contains 0 elements.
The value of the 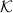 -anti-ancestral subset {A} is 6; the value of {B, E} is 3 + 1 = 4; the value of {C, E} is
4 + 1 = 5; the value of {D, G} is -1 + 1 = 0 and the value of {B, E, F} is 3 + 1 + (-5) = -2. Since the tree is
small, it’s easy to convince yourself by inspection that the maximum possible value of any
-anti-ancestral subset {A} is 6; the value of {B, E} is 3 + 1 = 4; the value of {C, E} is
4 + 1 = 5; the value of {D, G} is -1 + 1 = 0 and the value of {B, E, F} is 3 + 1 + (-5) = -2. Since the tree is
small, it’s easy to convince yourself by inspection that the maximum possible value of any 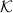 -anti-ancestral
subset is 6. However, notice that there might be several ways to achieve the maximum value: {A} and {C, E, G}
both have value 6. You are only asked to find the value of the maximum
-anti-ancestral
subset is 6. However, notice that there might be several ways to achieve the maximum value: {A} and {C, E, G}
both have value 6. You are only asked to find the value of the maximum 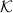 -anti-ancestral subset so it doesn’t
really matter how many of them exist.
-anti-ancestral subset so it doesn’t
really matter how many of them exist.
Input
The input file contains several test cases (at most 50).
Each test case is described on three lines:
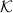 , the number of nodes in the tree and the parameter
, the number of nodes in the tree and the parameter 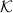 as explained above. Assume 2 ≤ N ≤ 105 and 1 ≤
as explained above. Assume 2 ≤ N ≤ 105 and 1 ≤ 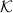 ≤ 100 (notice that these constraints guarantee
that there will always exist at least one
≤ 100 (notice that these constraints guarantee
that there will always exist at least one 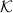 -anti-ancestral subset, e.g. by taking a single node). The
nodes will be numbered 0 through N - 1. The root of the tree will always be node 0. You can
assume that the tree will always be connected, i.e., there will always exist a path connecting any
pair of nodes.
-anti-ancestral subset, e.g. by taking a single node). The
nodes will be numbered 0 through N - 1. The root of the tree will always be node 0. You can
assume that the tree will always be connected, i.e., there will always exist a path connecting any
pair of nodes.
The last line contains two zeros and should not be processed.
See the sample input for clarification about this format. The first test case is the tree given in the figure above.
Output
For each test case, output one integer on a single line — the maximum possible value of any 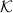 -anti-ancestral
subset.
-anti-ancestral
subset.
Sample input and output
|
standard input
|
standard output
|
|
7
3
6 3 4 -1 1 -5 1 0 1 1 0 0 5 2 1 -1 1 0 3 3 1 2 3 0 0 8 8 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 4 4 -27 -45 -67 -98 2 0 2 0 0 |
6
1 5 8 -27 |
1Formally, we say that node u is an ancestor of node v if u lies on the path from v to the root of the tree.