Handgun Shooting Sport 

Crystal billboards present snipers with the opportunity of shooting sports in the abandoned neighborhoods of Crystal City. One popular shooting sport for a sniper is to destroy all crystal billboards in front of a building. The rules of this game enforce the sniper to fix his/her gun to the ground of the building's roof, so it can rotate freely in any direction. However, once the gun is fixed, it cannot be placed in any other location. The goal of the game is to destroy all crystal billboards firing the minimum number of shots.

Every time the sniper fires, any crystal billboard in the way of the bullet is destroyed, even if the bullet only touches one extreme of the billboard. A bullet never changes direction or speed once it is fired, even if it destroys any crystal billboards.

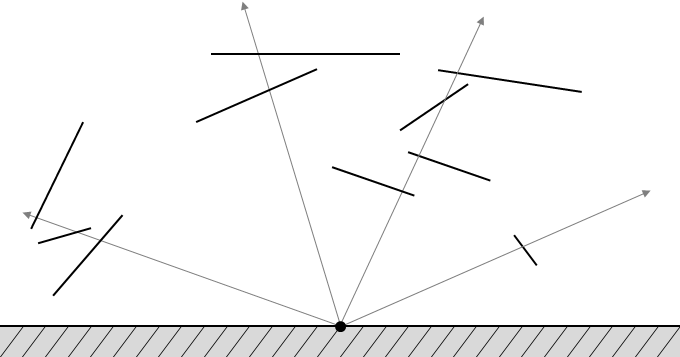
The following figure depicts a sniper in a fixed location facing a layout of ten crystal billboards. The sniper has destroyed all ten crystal billboards and has achieved the goal of the game because he/she destroyed all crystal billboards firing the minimum number of shots possible.

Given the initial location of a sniper and a layout of crystal billboards, your task is to determine the minimum number of shots that would destroy all crystal billboards.

Input 

The first line of the input contains a natural number B defining the number of crystal billboards in the shooting layout ( 1 $\leq$ B $\leq$ 10³). Each one of the following B lines contains four integer numbers x₁, y₁, x₂, y₂ separated by blanks, defining the coordinates of the line segment with extremes (x₁, y₁) and (x₂, y₂) ( -10³ $\leq$ x₁ $\leq$ 10³, 0 < y₁ $\leq$ 10³, -10³ $\leq$ x₂ $\leq$ 10³, 0 < y₂ $\leq$ 10³, y₁ ^. x₂ $\neq$ x₁ ^. y₂). You can assume that the shooting layout is modeled as the region on the Cartesian plane above the x-axis, that the sniper is located in the origin (0, 0), that each crystal billboard is represented with a line segment whose extremes are not collinear with the origin, and that no pair of crystal billboards intersects. The last test case is followed by a line containing a zero.

Output 

For each test case, a line must be printed with the minimum number of shots that fired from the sniper location would destroy all crystal billboards in the shooting layout.

Sample Input 

10
-309 98 -258 204
-303 83 -251 98
-218 111 -287 31
-145 204 -23 257
-129 272 59 272
-8 159 74 130
150 146 68 174
59 196 128 242
98 256 241 235
197 61 173 92
3
-100 10 -100 50
-50 100 50 100
100 10 100 50
5
-100 100 100 100
-80 120 80 120
-60 140 60 140
-40 160 40 160
-20 180 20 180
2
-50 50 0 50
-10 70 50 70
2
-50 50 0 50
0 70 50 70
2
-50 50 0 50
10 70 50 70
0

Sample Output 

4
3
1
1
1
2