Edgetown's Traffic Jams 

Edgetown is proudly a full-communicated city. That means that Edgetowners have decided that it must be possible to travel from any point in the city to any other point, using a car. Every point in Edgetown is located on a block, and every block connects two intersections (so that there are no intersections between a block nor two blocks connecting the same intersections). The city authorities have traditionally warranted this feature ensuring that the city plan is connected (i.e., there are not isolated intersections) and that some blocks are two-way.

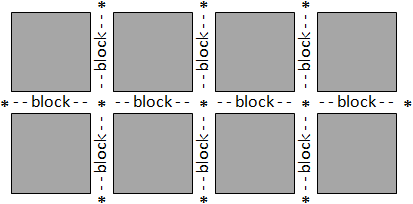
Given two intersections X and Y in Edgetown, the distance from X to Y is measured as the minimum number of blocks that should be traveled going from X to Y. The following diagram shows a possible configuration with eight blocks and eleven intersections (marked with asterisks).

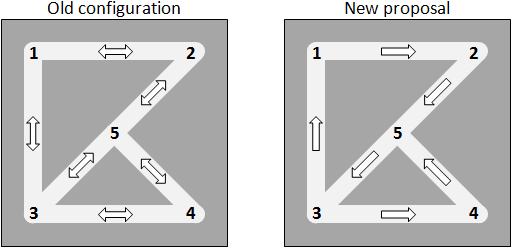
Lately there have been traffic jams at several points, almost at all times. Experts recommend a simple solution: just change some two-way blocks to be one-way blocks. However, it is clear that this should be done carefully, because accessibility among city points may be lost. On the other hand, even if accessibility is guaranteed, it is possible that distances between specific intersections may be significantly augmented.

After a lot of discussions, the Mayor's advisers have recommended to accept any proposal that increases the distance between any two intersections by a factor A augmented by a constant B, with respect to the old configuration (i.e., if the actual distance from one intersection to another is x, then the new distance should be at most A ^. x + B).

You are hired to develop a program to decide if a given proposal to orient city blocks satisfies the requirements.

Input 

There are several cases to analyze. Each case is described with a set of lines:

• The first line contains a non-negative integer n ( 3 $\leq$ n $\leq$ 100) that represents the number of intersections in Edgetown. Suppose that the intersections are identified by natural numbers in the set {1,..., n}.
• The line i + 1 ( 1 $\leq$ i $\leq$ n) begins with the number i and follows with a list of intersection numbers different from i (without repetitions). That means that the intersection i is connected by a block to each of the intersections numbered by elements in the list.
• The next n lines describe, with the same already specified format, the new proposal. In the description of the blocks in the proposal should be understood that the blocks are oriented going out from the first element in the line to each of the adjacent elements (the same fact applies to the old configuration).
• The case description ends with a line with two integer values A and B ( 0 $\leq$ A $\leq$ 10, 0 $\leq$ B $\leq$ 10).

The last test case is followed by a line containing a single `0'.

Output 

For each case print one line with the word `Yes' if the proposal satisfies the given requirements, or the word `No' otherwise. Answers should be left aligned.

Sample Input 

5
1 2 3
2 1 5
3 4 5 1
4 3 5
5 2 3 4
1 2
2 5
3 1 4
4 5
5 3
1 2
5
1 2 3
2 1 5
3 4 5 1
4 3 5
5 2 3 4
1 2
2 5
3 1 4
4 5
5 3
2 0
3
1 2
2 1 3
3 1 2
1 2
2 3
3 1
0 2
0

Sample Output 

Yes
No
Yes