Digital Roulette

John is developing a videogame that allows players to bet in a wall roulette. Players may bet for integer numbers from 0 to N, for some N $\ge$ 0 that represents the maximum number in the roulette.

Of course, the roulette behaves digitally. As a matter of fact, John designed its way to choose a value in the interval 0..N (the result of spinning the roulette) with a digital trigger that moves the roulette with a force that depends on an integer value x randomly chosen in the interval 0..M, where M $\ge$ 0 (M is the maximal appliable force). The roulette turns around a distance equivalent to P(x), where P is a polynomial with integer coefficients. One distance unit represents a displacement of one roulette number, counting clockwise.

It is clear that some result values may be produced by different chosen force values. Also, depending on the mechanism parameters, some numbers in the roulette may be not attainable regardless of the force value. For example, if N = 7, M = 5 and P(x) = x² + 1, the mechanism can generate only three different results:

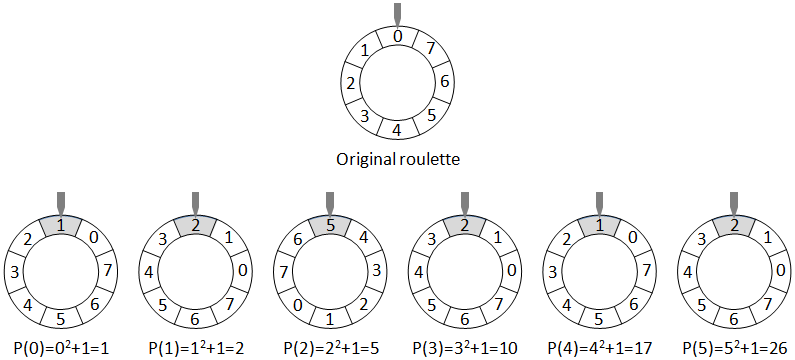
$\epsfbox{p12318.eps}$

John wants to know how many different result values may be attained by his mechanism. Can you help him?

Input

There are several cases to analyze. Each case is described by three lines:

The first line contains two non-negative integer numbers N and M, separated by a blank ( 1 $\leq$ N $\leq$ 10⁷, 0 $\leq$ M $\leq$ 10⁵).
The second line contains an integer k, the grad of the polynomial P ( 0 $\leq$ k $\leq$ 10).
The third line contains k + 1 integers a₀, a₁,..., a_k separated by blanks, indicating the integer coefficients that define the polynomial P, i.e., P(x) = a_kx^k + ^... + a₁x + a₀. You can assume that 0 $\leq$ a_i $\leq$ N for each 0 $\leq$ i $\leq$ k. If k > 0 then you may assume that a_k $\neq$ 0.

The last test case is followed by a line containing two zeros.

Output

For each case, print one line indicating how many different numbers are attainable by John's mechanism.

Sample Input

Sample Output