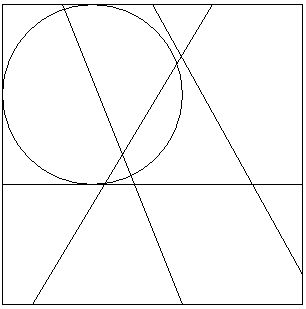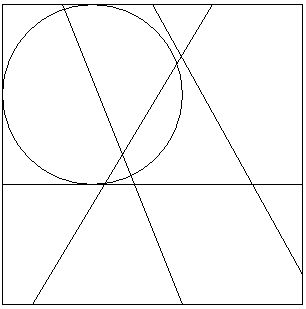There is a rectangle on the Cartesian plane, whose bottom-left corner is (0, 0), top-right corner is
(L, W). You draw some line segments to divide the rectangle into pieces. Each line segment connects
two points on the boundary of the original rectangle (these two points are guaranteed to be on different
sides of the rectangle).
Finally, you draw some discs (a disc is a circle with its interior), and your task is to find out all the
pieces each disc is intersecting with (i.e. pieces that have non-zero intersection area with the disc), and
output their areas in increasing order. An example picture is shown below:
There will be at most 100 test cases. Each test case begins with four integer n, m, L, W (
1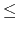 n, m
n, m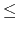 20,
1
20,
1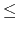 L, W
L, W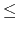 100), where n is the number of line segments, m is the number of discs. Each of the next n
lines describes a line segment with for integers x1, y1, x2, y2, that is a segment connecting (x1, y1) and
(x2, y2). These two points are guaranteed to be on different sides of the original rectangle. Each of the
last m line contains three integers x, y, R (
0
100), where n is the number of line segments, m is the number of discs. Each of the next n
lines describes a line segment with for integers x1, y1, x2, y2, that is a segment connecting (x1, y1) and
(x2, y2). These two points are guaranteed to be on different sides of the original rectangle. Each of the
last m line contains three integers x, y, R (
0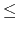 x
x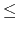 L,
0
L,
0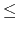 y
y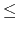 W,
1
W,
1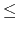 R
R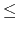 100), indicating that the disc is
centered at (x, y), whose radius is R. No two segments will be the same. Input is terminated by
n = m = L = W = 0.
100), indicating that the disc is
centered at (x, y), whose radius is R. No two segments will be the same. Input is terminated by
n = m = L = W = 0.
For each disc (same order as in input), print the number of pieces that the disc is intersecting with, and
the areas of these pieces in a single line. The areas should be sorted in increasing order, and each area
should be rounded to 2 digits after the decimal point. Print a blank line after each test case.
4 1 10 10
0 4 10 4
1 0 7 10
5 10 10 1
2 10 6 0
3 7 3
0 0 0 0
4 0.50 10.03 10.77 18.70
The Seventh Hunan Collegiate Programming Contest
Problemsetter: Rujia Liu, Special Thanks: Jane Alam Jan