Optimal Symmetric Paths 

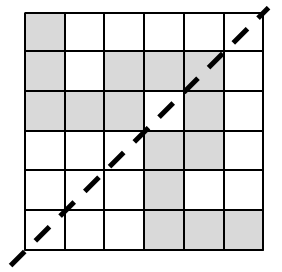
You have a grid of n rows and n columns. Each of the unit squares contains a non-zero digit. You walk from the top-left square to the bottom-right square. Each step, you can move left, right, up or down to the adjacent square (you cannot move diagonally), but you cannot visit a square more than once. There is another interesting rule: your path must be symmetric about the line connecting the bottom-left square and top-right square. Below is a symmetric path in a 6 x 6 grid.

Your task is to find out, among all valid paths, how many of them have the minimal sum of digits?

Input 

There will be at most 25 test cases. Each test case begins with an integer n ( 2$\le$n$\le$100). Each of the next n lines contains n non-zero digits (i.e. one of 1, 2, 3, ..., 9). These n² integers are the digits in the grid. The input is terminated by a test case with n = 0, you should not process it.

Output 

For each test case, print the number of optimal symmetric paths, modulo 1,000,000,009.

Sample Input 

2
1 1
1 1
3
1 1 1
1 1 1
2 1 1
0

Sample Output 

2
3

The Seventh Hunan Collegiate Programming Contest
Problemsetter: Rujia Liu, Special Thanks: Yiming Li & Jane Alam Jan