B: Balanced ScoreCard

The Balanced ScoreCard (BSC), first introduced by Robert Kaplan and David Norton, is a strategic planning and management system that is used extensively in organizations worldwide (industry, business, government and nonprofit) primarily to monitor individual and organizational performance against strategic goals. The BSC provides a tree-shaped hierarchical view of the status of every objective required to fulfill a specific organization goal. The root of the tree denotes the organization goal itself whereas the leaves refer to the most specific objectives (performance of an employee, sales of a specific product); inner nodes denote objectives per organizational area (business unit, department, product line, customers from a specific region).

The performance of a given organization goal is in terms of what was expected to be done and what was actually done. This relationship is known as the result of and has to be calculated from the bottom-up. Every objective in the lowest level of the tree has a predefined expected value and a post-defined actual value. The percentile relationship between the actual and expected values gives the result of the objective. The result of inner objectives (including the root) is calculated according to a rule given to every objective. Typical rules include the following: 1) the result of an objective is the weighted average of the results of the children objectives, 2) the result of an objective is the worst result of the children objectives. To implement the first rule, objectives have to be accompanied with a weight value given as a percentage. To illustrate better this, consider the following example:

General rule = 2

Weight = 50%, rule = 1

1.1

Weight = 60%, value = 95.0

1.2

Weight = 30%, value = 85.0

1.3

Weight = 10%, value = 63.0
2. Weight = 50%, rule = 2

1.1

Weight = 50%, value = 72.0

1.2

Weight = 50%, value = 92.0

The result of the organization goal is then calculated as follows:

Result	=	min{((95.0 `x` 0.60) + (85.0 `x` 0.30) + (63.0 `x` 0.10), min{72.0, 92.0}}
	=	min{88.8, 72.0} = 72.0

Notice that weight values are ignored when parent's rule is 2.

The problem consists in figuring out the result of an organization goal, given a BSC containing:

1): The weight and the result, for every lowest-level objective
2): The weight, the rule and the children objectives, for every inner objective.

And assuming the BSC is well-formed (no syntactic errors are expected).

Nevertheless, the BSC may be unbalanced: the sum of the weight of a given group of sibling objectives is not equals to 100.0% $\pm$ 0.01, no matter the parent's rule.

Input

The first line contains an integer number, N > 0, denoting the number of test cases.

The next N lines contain each the definition of an organization goal, having the following syntax:



< rule > < blank > < objective > { < blank > < objective > }^*, where: 

< rule > is either 1 or 2, and follows the definition explained above. 

< blank > is a blank space  


< objective > can be either 
< leaf - objective > or 
< inner - objective > 


{}^* denotes 0 or more occurrences of  


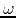
< leaf - objective > is written as: 
< ( > < weight > < ; > < value > < ) > 

< weight > is a number greater than 0.0 but not greater than 100.0  

< value > is a number between 0.0 and 100.0  


< ( > is the symbol (  


< ) > is the symbol )  


< ; > is the symbol ;  


< inner - objective > is written as:  


< ( > < weight > < ; > < rule > < ; > < { > < objective > { < , > < objective > }^* < } > < ) > 


< { > is the symbol {  


< } > is the symbol }

Output

The output consists of N lines, where every line k $\le$ N contains a number in the range [0.0 ...100.0] which denotes the result of organization goal k. Keep only the two most significant decimals. If the BSC k is not balanced, line k contains the word `Unbalanced' instead.

Sample Input

3
1 (35;95) (65;78)
1 (72;83) (28;1;{(60;100),(30;97),(15;85)})
2 (50;1;{(60;95),(30;85),(10;63)}) (50;2;{(50;72),(50;92)})

Sample Output

83.95
Unbalanced
72.00