One of the primary hobbies (and research topics!) among Computing Science students at the University of Alberta is, of course,
the playing of games. People here like playing games very much, but the problem is that the games may get solved completely--as
happened in the case of Checkers. Generalization of games is the only hope, but worries that they will be solved linger still.
Here is an example of a generalization of a two player game which can also be solved.
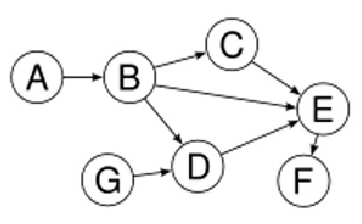
Suppose we have a directed acyclic graph
with some number of stones at each node. Two players take turns moving a stone from any node to one of its neighbours, following
a directed edge. The player that cannot move any stone loses the game. Note that multiple stones may occupy the same node at any given time.
The input consists of a number of test cases. Each test case begins with a line containing two integers n and m, the number of nodes
and the number of edges respectively. (
1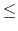 n
n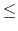 1000,
0
1000,
0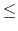 m
m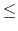 10000). Then, m lines follow, each containing two
integers a and b: the starting and ending node of the edge (nodes are labeled from 0 to n - 1).
10000). Then, m lines follow, each containing two
integers a and b: the starting and ending node of the edge (nodes are labeled from 0 to n - 1).
The test case is terminated by n more
integers
s0,..., sn-1 (one per line), where si represents the number of stones that are initially placed on node i
(
0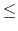 si
si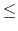 1000).
1000).
Each test case is followed by a blank line, and input is terminated by a line containing `0 0' which should not be processed.
For each test case output a single line with either the word `First' if the first player will win, or the word `Second'
if the second player will win (assuming optimal play by both sides).
4 3
0 1
1 2
2 3
1
0
0
0
7 7
0 1
0 2
0 4
2 3
4 5
5 6
4 3
1
0
1
0
1
0
0
0 0
First
Second

![]() si
si![]() 1000).
1000).