Problem B
Bisectors
Input: Standard Input
Output: Standard Output
We all probably know how to find equation
of bisectors in Coordinate Geometry. If the equations of two lines are ![]() and
and ![]() , then the equations of the bisectors of the four angles they
create are given by
, then the equations of the bisectors of the four angles they
create are given by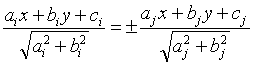 . Now one has to be quite intelligent to find out for which
angles to choose the ‘+’(plus) sign and for which angles to choose the
‘-’(minus) sign. You will have to do similar sort of choosing in this problem.
Suppose there is a fixed point (Cx, Cy) and there are n
(n≤10000) other points around it. No two points from these n points are
collinear with (Cx, Cy). If you connect all these point
with (Cx, Cy) you will get a star-topology like image
made of n lines. The equations of these n lines are also given and only these
equations must be used when finding the equation of bisectors. This n lines
create n(n-1)/2 acute or obtuse angles in total and so they have total n(n-1)/2
bisectors. You have to find out how many of these bisectors have equations
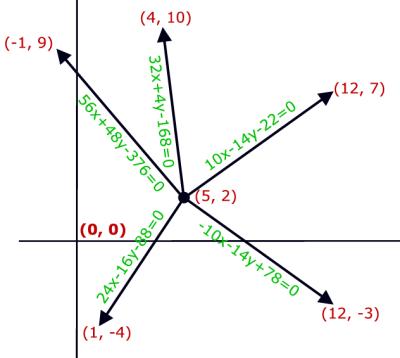
formed using the + sign. The image below shows an image where n=5, Cx=5
and Cy=2. This image corresponds to the only sample input.
. Now one has to be quite intelligent to find out for which
angles to choose the ‘+’(plus) sign and for which angles to choose the
‘-’(minus) sign. You will have to do similar sort of choosing in this problem.
Suppose there is a fixed point (Cx, Cy) and there are n
(n≤10000) other points around it. No two points from these n points are
collinear with (Cx, Cy). If you connect all these point
with (Cx, Cy) you will get a star-topology like image
made of n lines. The equations of these n lines are also given and only these
equations must be used when finding the equation of bisectors. This n lines
create n(n-1)/2 acute or obtuse angles in total and so they have total n(n-1)/2
bisectors. You have to find out how many of these bisectors have equations
formed using the + sign. The image below shows an image where n=5, Cx=5
and Cy=2. This image corresponds to the only sample input.
|
|
|||
|
Figure: Five lines above create 5(5-1)/2=10 angles and
these angles has 10 bisectors. Of these 10 bisectors, the equation of only 4 are
formed using the + sign of the formula |
Input
The input file contains maximum 35 sets of inputs. The description of each set is given below:
First line of each set contains three integers Cx, Cy (-10000 ≤ Cx, Cy ≤ 10000) and n (0 ≤ n ≤
10000). Each of the next n lines
contains two integers xi, yi (20000 ≤ xi, yi ≤ 20000) and a string
of the form aix+biy+ci=0. Here (xi, yi) is the coordinate of a point around
(Cx, Cy) and the string denotes the equation of the line segment formed by
connecting (Cx, Cy) and (xi, yi). You can assume
that (-100000 ≤ ai,
bi ≤ 100000)
and (-2000000000 ≤ ci
≤ 2000000000). This equation will actually be used to find the equations
of bisectors of the angles that this line creates.
Input is terminated by a set where the value of n is zero.
Output
For each
set of input produce one line of output. This line contains an integer
number P that denotes of the ![]() bisector equations how many are formed using
the + sign in the bisector equation
bisector equations how many are formed using
the + sign in the bisector equation 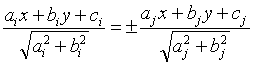 .
.
|
Sample Input |
Output for Sample Input |
|
5 2 5 12 7
10x-14y-22=0 1 -4
24x-16y-88=0 4 10
32x+4y-168=0 -1 9
56x+48y-376=0 12 -3
-10x-14y+78=0 10 10 0 |
4 |
Problemsetter: Shahriar
Manzoor
Special Thanks: Derek
Kisman