I

Rectangle of Permutation

Input: Standard Input

Output: Standard Output

 

We want to build a rectangle where each row is a permutation of 0 to N-1.  We want to make this rectangle with as many rows as possible while maintaining the following constraints.     

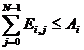 and , where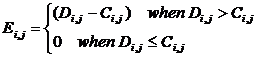

 is the number of occurrences of integer j in the column i. C is a matrix of N rows and N columns will be given as input. A and B are two sequences of size N will be given as input. Given N, A, B, C build a rectangle with the largest possible number of rows.

 

Input

First line of the input contains T () the number of test cases. Then T test cases follows. Each test case starts with an integer N () indicates the number of columns in the rectangle. Next Line contains N integers seperated by a single space. These integers are A0 to AN-1 (). Next line contains N integers separated by a single space. These integers are B0 to BN-1 (). Each of the next N line contains N integers in each lines. The integer on row i and column j is Ci,j () ( i and j starts from zero). A blank line will follow each test case.

 

Output

For each test case the first line of the output will be in the following format “Case #C: R”. Quotes are for clarity only. C is the test case number starting from 1. R is the maximum possible rows of the rectangle. Each of the next R lines should contain N integer in each line seperated by spaces. Each of these  N integers in each line should be a permutation of 0 to N-1. The whole RXN rectangle should maintain the constraints as described in the problem statement.

 

Sample Input                                             Output for Sample Input

2

3

0 0 0

0 0 0

2 0 0

0 2 0

0 0 2

 

3

1 2 3

3 2 1

1 2 3

2 3 1

3 1 2

 

Case 1: 2

0 1 2

0 1 2

Case 2: 7

0 1 2

1 0 2

1 0 2

2 1 0

2 1 0

2 1 0

0 2 1

 

Problemsetter: Abdullah al Mahmud, Special Thanks: Derek Kisman, Mohammad Mahmudur Rahman