Rational Billiard 

The International Billiard Manufactory (IBM) builds the best billiard tables in the world. Its last product is the Rational Billiard, which is a friction-less table with volume-less balls. This means that balls just occupy a point in the space, and once they are struck with the cue, they move on the table with constant velocity, until they hit another ball.


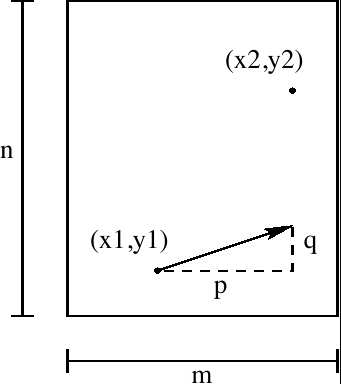
IBM wants you to build a program to analyse the behavior of balls in the Rational Billiard. The program has to decide whether a ball, struck with certain angle, will hit another ball in certain position. The next figure shows the configuration of the table and the balls:

\epsfbox{p11657.eps}

m and n are integer values that indicate the size of the table. (x1, y1) and (x2, y2) are the coordinates of the first and second ball respectivelly, with 0 < x1, x2 < m and 0 < y1, y2 < n. The direction in which the first ball is struck is determined by the integer values p and q. More precisely, the slope $ {\frac{{q}}{{p}}}$ determines the hitting direction of the cue, where p and q cannot be zero simultaneously. A value of p = 0 means that the ball moves parallel to the vertical axis, according to the sign of q. When the ball hits an edge, it rebounds like if the edge were a mirror ( incidence angle = reflection angle). In the special case when the ball hits a corner, it is reflected on the same line but in the opposite direction of arrival. Finally, spin effects are neglected, too.

Input 

Each line in the input corresponds to a test case specified by eight integer values: m, n, x1, y1, x2, y2, p and q, with 0 < m, n$ \le$1000, 0 < x1, x2 < m, 0 < y1, y2 < n, -1000$ \le$p, q$ \le$1000, and | p| + | q| > 0.

The end of the input is specified by a line with the string ``0 0 0 0 0 0 0 0''.

Output 

For each test case, the program must output a line with the the text ``HIT'' if the first ball hits the second ball, or ``MISS'' if it does not.

Sample Input  

4 4 3 1 1 1 1 1
4 4 3 1 2 2 1 1
0 0 0 0 0 0 0 0

Sample Output  

HIT
MISS