Message in the Enemy Territory 

A group of commandos has been caught and sent to a maximum-security prison in enemy territory. In order to escape from the prison, a soldier needs to give a message to the squadron leader.

The boundary of the prison is protected by electronic alarms: for his security, the soldier needs to keep a distance greater than m from the boundary. An additional restriction is that the soldier can only stand on those positions with integer coordinates. In each step, the soldier can move, from a given position (x, y), only to the nearby positions: (x - 1, y - 1), (x - 1, y), (x - 1, y + 1), (x, y - 1), (x, y + 1), (x + 1, y - 1), (x + 1, y) and (x + 1, y + 1), without going out of the interior of the prison. 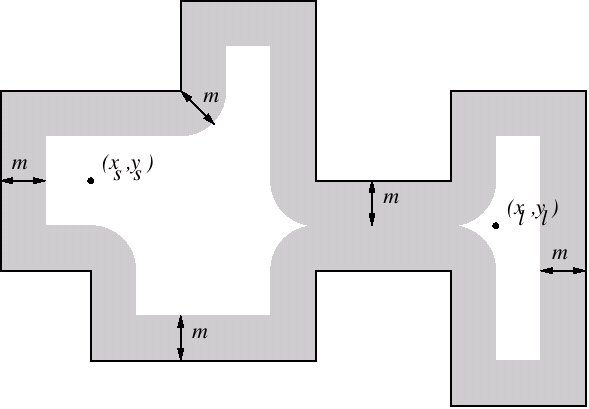The walls of the prison form a simple polygon (no repeated vertices and no intersections between edges) and all of them are parallel to either the x-axis or the y-axis of a hypothetical coordinate system. The following figure shows a typical prison's plan:

(x_s, y_s) and (x_l, y_l) corresponds to the position of the soldier and the squadron leader respectively. The gray area indicates those positions that are at distance less than or equal to m from the prison's boundary, i.e., the zone that the soldier cannot stand on.

A safe path is a sequence of pairs of integer coordinates, each one at a distance greater than m from the boundary of the prison, so that consecutive pairs are different and do not differ in more than one in each coordinate. In the depicted example, there is not a safe path from the soldier to the squadron leader.

Your task is to determine, for a given prison's plan, if there exists a safe path from the soldier position to the squadron leader position.

Input 

The problem input consists of several test cases. Each test case consists of three lines:

• The first line contains two integer numbers separated by blanks, n and m, with 4$\le$n$\le$1000 and 1$\le$m$\le$30, indicating the number of the prison's boundary vertices and the alarm range respectively.
• The second line contains a list of 2 ^. n integer numbers, x₁, y₁,..., x_n, y_n, separated by blanks: the list of vertices of a simple n-polygon that describes the boundary of the prison. 0$\le$x_i, y_i$\le$1000.
• The last line contains four integer numbers separated by blanks, x_s, y_s, x_l, and y_l, indicating the position of the soldier and the position of the squadron leader ( 0$\le$x_s, y_s$\le$1000, 0$\le$x_l, y_l$\le$1000).

The end of the input is indicated by a line with ``0 0''.

Output 

For each test case the output includes a line with the word ``Yes'' if there exists a path from the soldier to the squadron leader. Otherwise the word ``No'' must be printed.

Sample Input 

4 1
0 0 0 5 5 5 5 0
2 2 3 3
8 3
0 16 0 6 4 6 4 0 12 0 12 10 8 10 8 16 
4 12 8 4  
0 0

Sample Output 

 
Yes
No