Working at the Restaurant 

Last night, Tom went on a date with a really nice girl. However, he forgot to take his credit card with him and he had no cash in his wallet, so he ended up working at the restaurant to pay for the bill. His task is to take plates from the waiter when he comes from the tables, and pass them along when the diswasher requests them. It is very important for the plates to be washed in the same order as they are brought from the tables, as otherwise it could take too long before a plate is washed, and leftover food might get stuck. Trying to hold all the plates in his hands is probably not a great idea, so Tom puts them on a table as soon as the waiter hands them over to him, and picks them up from the table again when the time comes to pass them along to the dishwasher. There is space for only two piles of plates on the table, which will be referred to as pile 1 and pile 2. There is only one table Tom can use.

Tom won last year's SWERC, so he is certainly capable of optimizing for efficiency. You have to output a transcript of one possible way in which Tom might decide to organize the plates on the table during the process, given the sequence of plates and requests he receives.

Input 

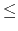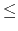The input has several test cases. Each case begins with a line containing a number N ( 1 $ \leq$ N $ \leq$ 1 000), followed by N lines, which contain either DROP m or TAKE m, where m > 0 is the number of plates to take or drop. DROP m represents that the next event is the waiter bringing m plates to Tom, one by one, so he has to drop them on the table; TAKE m represents that the next event is Tom taking m plates from the table, one by one, and passing them along in the right order. You can assume that he never receives a TAKE m instruction when there are fewer than m plates on the table, and that the sum M of all values of m corresponding to DROP operations does not exceed 100 000. Note that there might be plates left on Tom's table when the last request is issued, as Tom might be relieved of his duty to stay until the restaurant closes.

The input ends with a line with N = 0, which must not be processed.

Output 

For every test case, the output will be a series of lines describing the operations to be performed with the plates. The content of each line will be one of the following:

You must output at most 6N lines, and the total number of movements of plates in your transcript (that is, the sum of the m's printed in your output, for all three kinds of operations), must be at most 6M, as otherwise Tom won't be able to cope with all the work.

Note that Tom must obey the commands in the same order as they are issued. This means that, if he receives a TAKE m command, he must perform a certain number of MOVE and TAKE operations such that the sum of the numbers of plates taken adds up exactly to m before performing the operations corresponding to the next command; and if he receives a DROP m command, he must perform a number of DROP or MOVE operations for which the sum of the numbers of plates dropped adds up exactly to m before performing the operations corresponding to the next command.

Of course, it is also forbidden to take plates from the waiter or pass them along to the dishwasher in the absence of the corresponding order.

There must be an empty line between the outputs of different cases.

Any solution satisfying these conditions will be accepted.

Sample Input  

3
DROP 100
TAKE 50
TAKE 20
3
DROP 3
DROP 5
TAKE 8
0

Sample Output  

DROP 2 100
MOVE 2->1 100
TAKE 1 50
TAKE 1 20

DROP 2 3
DROP 2 5
MOVE 2->1 8
TAKE 1 8