Problem B
First Knight

Archibald and Adalbert are inseparable friends and the best knights of the whole kingdom. Competitive as they are, they occasionally engage in a little open-air sword fight, just to determine who among them really is the first knight. Of course, neither Adalbert nor Archibald wins, but they keep themselves busy for quite a while and get around in the surroundings. You have to calculate about how long their next `fight' will last.

All the action takes place in a rectangular area which, for the sake of simplicity, is divided into unit squares numbered from $(1,1)$ to $(m,n)$ . Starting at $(1,1)$ , the knights move from one square to one of the at most four adjacent squares, and finish as soon as they reach $(m,n)$ where the tavern is located. At each square, it is largely a matter of chance where the fight will continue, but it also depends on the environment (for example, if a certain direction is uphill). Our model uses probabilities to decide into which adjacent square the fight will move next. (For example, an uphill direction has a lower probability.) It is your job to calculate the expected number of moves that are needed before the tavern is reached. You can assume that every move is independent of the directions chosen in the previous moves.

Input
The input consists of a sequence of rectangular areas. Each area starts with a line containing the dimensions of the rectangle $m$ and $n$ , where $1 \leq m, n \leq 40$ . Four blocks follow that state the probability of a move in each direction. Every block contains $m$ lines, and each line contains $n$ numbers $p_{i,j}^{(k)}$ , where $0 \leq p_{i,j}^{(k)} \leq 1$ for all $1 \leq i \leq m$ and $1 \leq j \leq n$ and $1 \leq k \leq 4$ . The probabilities in block $k$ are arranged as follows:

$$\begin{array}{llllll} p_{1,1}^{(k)} & p_{1,2}^{(k)} & p_{1,3}^{(k... ...{(k)} & p_{m,3}^{(k)} & \dots & p_{m,n-1}^{(k)} & p_{m,n}^{(k)} \\ \end{array}$$

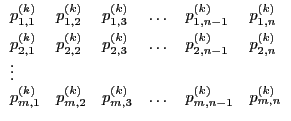
The number $p_{i,j}^{(k)}$ gives the probability of a move from square $(i,j)$ to the next square: In block $1$ this is $(i{+}1,j)$ , in block $2$ it is $(i,j{+}1)$ , in block $3$ it is $(i{-}1,j)$ and in block $4$ it is $(i,j{-}1)$ . For each square $(i,j)$ except the tavern $(m,n)$ , the probabilities $p_{i,j}^{(k)}$ add up to $1$ and at least one of $p_{i,j}^{(1)}$ or $p_{i,j}^{(2)}$ is not 0 . (This ensures that the tavern will finally be reached with probability $1$ .) You may assume that the probability of moving outside the rectangle is 0 , as are $p_{m,n}^{(k)}$ for all $k$ . The sequence of areas is followed by a line containing two zeros.

Output
For each area, output a line containing the expected number of moves from $(1,1)$ to $(m,n)$ . This number must have an absolute error less than $0.1$ compared to the exact answer that is always less than $1000000$ .

Sample Input

2 2
0.01 0.50
0.00 0.00
0.99 0.00
0.50 0.00
0.00 0.00
0.50 0.00
0.00 0.50
0.00 0.00
1 5
0.0 0.0 0.0 0.0 0.0
1.0 0.1 0.7 0.5 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.9 0.3 0.5 0.0
3 3
0.000001 0.0 1.0
0.0 1.0 1.0
0.0 0.0 0.0
0.999999 1.0 0.0
1.0 0.0 0.0
0.000001 0.000001 0.0
0.0 0.0 0.0
0.0 0.0 0.0
0.999999 0.0 0.0
0.0 0.0 0.0
0.0 0.0 0.0
0.0 0.999999 0.0
0 0
 

Sample Output

4.0
41.142857142857146
7.999994000002